Two Sample Nonparametric Test: Mann-Whitney Test - Exact (with 2 Sample KS Option)
We will redo the example for the Two Sample Mann-Whitney Test (with 2 Sample KS Option) to compute exact P-Values. Typically, this would not be necessary unless the sample sizes were smaller (each sample N <= 10 for Mann-Whitney), but this gives us continuity on the example. Due to the large number of permutations, we will use Monte Carlo Exact for this analysis and will consider a small sample problem later.
- Open Customer Data.xlsx, click Sheet 1 tab (or press F4 to activate last worksheet).
- Click SigmaXL > Statistical Tools > Nonparametric Tests - Exact > 2 Sample Mann-Whitney - Exact. If necessary, check Use Entire Data Table, click Next.
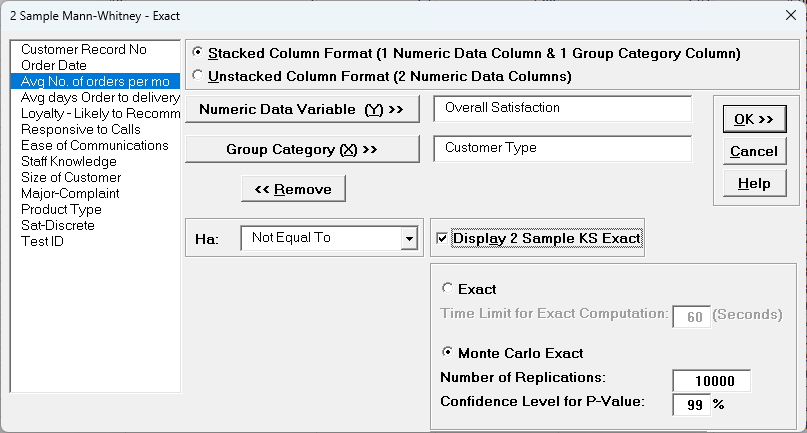
- With Stacked Column Format checked, select
Overall Satisfaction, click Numeric Data Variable (Y) >>; select
Customer Type, click Group Category (X) >> and Ha:
Not Equal To.
Select Monte Carlo Exact with the default
Number of Replications = 10000 and Confidence Level for P-Value
= 99%.
Check Display 2 Sample KS Exact.
Tip 1: If Exact is selected and the computation time limit is exceeded, a dialog will prompt you to use Monte Carlo or to increase the computation time.
Tip 2: 10,000 replications will result in a Monte Carlo P-Value that is typically correct to two decimal places. One million (1e6) replications will result in three decimal places of accuracy and typically require less than 60 seconds to solve for any data set.
Tip 3: The Monte Carlo 99% confidence interval for P-Value is not the same as a confidence interval on the test statistic due to data sampling error. The confidence level for the hypothesis test statistic is still 95%, so all reported P-Values less than .05 will be highlighted in red to indicate significance. The 99% Monte Carlo P-Value confidence interval is due to the uncertainty in Monte Carlo sampling, and it becomes smaller as the number of replications increases (irrespective of the data sample size). The Exact P-Value will lie within the stated Monte Carlo confidence interval 99% of the time.
The KS (Kolmogorov Smirnov) Exact test is only available for Monte Carlo Exact. - Click OK. Select Customer Type 2 and 3. Click OK. The resulting output for the 2 Sample Mann-Whitney - Monte Carlo test is:
- The resulting output for the 2 Sample KS - Monte Carlo test is:
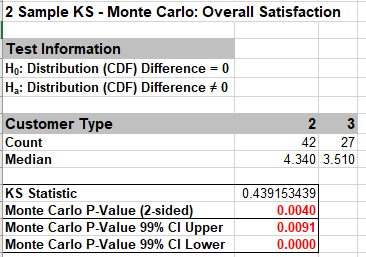
Given the Monte Carlo P-Value of .004 with 99% confidence interval 0.0000 to 0.0091, we reject H0 and conclude that Satisfaction distributions are significantly different between Customer types 2 and 3. As with the Mann-Whitney, the Monte Carlo P-Value is very close to the above “large sample” or “asymptotic” result. - Now we will consider a small sample problem. Open Stimulant Test.xlsx. This data is from:
Narayanan, A. and Watts, D. “Exact Methods in the NPAR1WAY Procedure,” SAS Institute Inc., Cary, NC. http://support.sas.com/rnd/app/stat/papers/exact.pdf
Researchers conducted an experiment to compare the effects of two stimulants. Thirteen randomly selected subjects received the first stimulant, and six randomly selected subjects received the second stimulant. The reaction times are in minutes. We will test the null hypothesis of no difference between the medians of the two stimulants against the alternative that stimulant 1 has smaller median reaction time than stimulant 2. - Select Reaction Time tab. Click SigmaXL > Statistical Tools > Nonparametric Tests – Exact > 2 Sample Mann-Whitney - Exact. If necessary, check Use Entire Data Table, click Next.
- With Stacked Column Format checked, select Reaction Time, click Numeric Data Variable (Y) >>; select Stimulant, click Group Category (X) >>; and Ha: Less Than.
Select Exact with the default Time Limit for Exact Computation = 60 seconds.
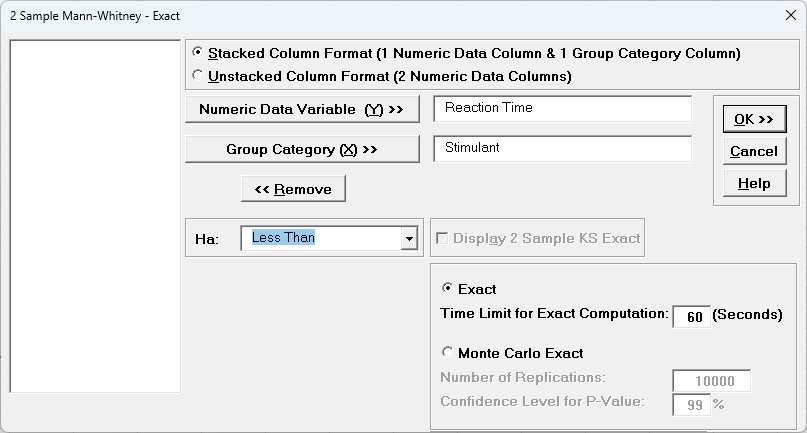
The 2 Sample KS Exact option is only available for Monte Carlo, so is greyed out. - Click OK. Select Stimulant 1 and 2.
This sets the order for the one-sided test, so the alternative hypothesis Ha is Median 1 < Median 2. - Click OK. Results:
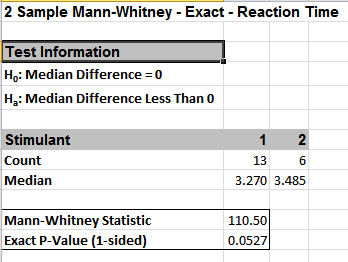
With the P-Value = .0527 we fail to reject H0, so cannot conclude that there is a difference in median reaction times. This exact P-Value matches that given in the reference paper.
By way of comparison, we will now rerun the analysis using the “large sample” or “asymptotic” Mann-Whitney test. - Select Reaction Time tab (or press F4 to activate last worksheet). Click SigmaXL > Statistical Tools > Nonparametric Tests – Exact > 2 Sample Mann-Whitney. If necessary, check Use Entire Data Table, click Next.
- With Stacked Column Format checked, select
Reaction Time, click Numeric Data Variable (Y) >>;
select Stimulant, click Group Category (X) >>;
and Ha: Less Than. Display 2 Sample KS is left unchecked.
- Click OK. Select Stimulant 1 and 2. Click OK. Results:
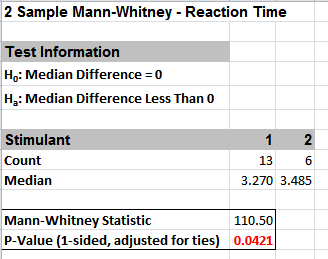
Now with the P-Value = .0421 we incorrectly reject H0.
The difference between exact and large sample P-Value is small but it was enough to lead us to falsely conclude that stimulant 1 resulted in a reduced median reaction time.
In conclusion, whenever you have a small sample size and are performing a nonparametric test, always use the Exact option.
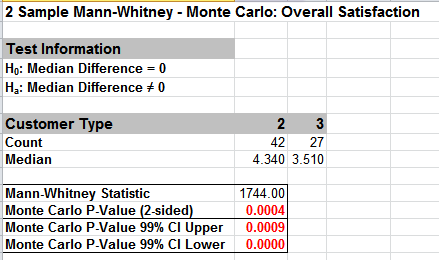
Given the Monte Carlo P-Value of .0004 we reject H0 and conclude that Median Customer Satisfaction is significantly different between Customer types 2 and 3. The Monte Carlo P-Value is very close to the above “large sample” or “asymptotic” result. This was expected because the sample size is reasonable (each sample N > 10), so the “large sample” P-Values are valid using a normal approximation for the Mann-Whitney Statistic.
The Monte Carlo P-Value 99% confidence interval is 0.0000 to 0.0009. Note that the Monte Carlo P-Value will be slightly different every time it is run (the Monte Carlo seed value is derived from the system clock). This was demonstrated using 10,000 replications, but with a P-Value this low, it is recommended that the number of replications be increased to 1e5 or 1e6 to get a better estimate.
Web Demos
Our CTO and Co-Founder, John Noguera, regularly hosts free Web Demos featuring SigmaXL and DiscoverSim
Click here to view some now!
Contact Us
Phone: 1.888.SigmaXL (744.6295)
Support: Support@SigmaXL.com
Sales: Sales@SigmaXL.com
Information: Information@SigmaXL.com