It is well known that the central limit theorem enables the t-Test and ANOVA to be fairly robust to the assumption of normality. A question that invariably arises is, “How large does the sample size have to be?” A popular rule of thumb answer for the one sample t-Test is “n = 30.” While this rule of thumb often does work well, the sample size may be too large or too small depending on the degree of non-normality as measured by the Skewness and Kurtosis. Furthermore it is not applicable to a One Sided t-Test, 2 Sample t-Test or One Way ANOVA.
To address this issue, we have developed a unique template that gives a minimum sample size needed for a hypothesis test to be robust.
Click SigmaXL > Templates & Calculators > Basic Statistical Templates > Minimum Sample Size for Robust Hypothesis Testing to access this template. It includes minimum sample size for robustness for the 1 Sample t-Test, 2 Sample t-Test and the One Way ANOVA.
The user may specify the alternative hypothesis as “Less Than” (one sided), “Not Equal To” (two sided) or “Greater Than” (one sided). Confidence levels of 90% (α = 0.1), 95% (α = .05) or 99% (α = .01) may also be specified:
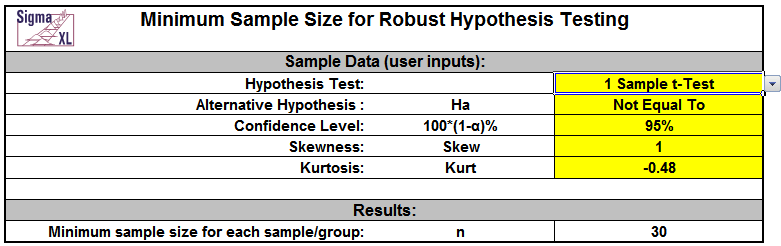
To use the template, simply select the appropriate Hypothesis Test, Alternative Hypothesis and Confidence Level using the drop down selection. Enter Skewness and Kurtosis values as shown in the yellow highlighted cells.
Note that in the example shown, the rule of thumb for a 1 Sample t-Test “n = 30” is confirmed with a moderate skew value of 1.
Now change the Alternative Hypothesis to “Less Than” and Confidence Level to 99% as shown:
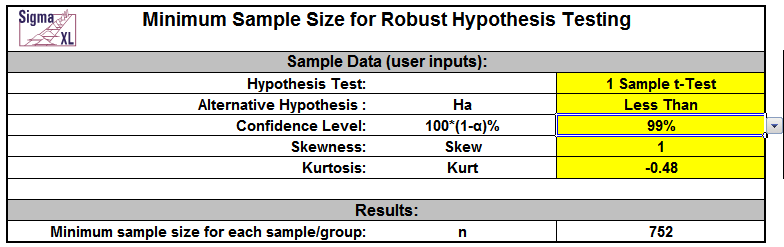
The minimum sample size required for robustness is now 752!
On the other hand, if you want to perform a standard One Way ANOVA, enter the values as shown:
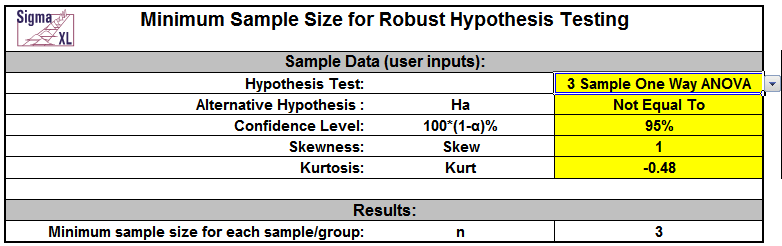
Now the minimum sample size requirement is only 3. This value applies to each sample or group, so for the 3 Sample ANOVA that would mean each sample has n = 3 for a total number of observations = 9.
Note that this calculator is strictly addressing the question of alpha robustness to non-normality. Power is not considered here.
If the minimum sample size requirements cannot be met, you should use a nonparametric equivalent to the parametric hypothesis test (i.e. One Sample Sign or Wilcoxon, Two Sample Mann-Whitney, Kruskal-Wallis or Mood’s Median: SigmaXL > Statistical Tools > Nonparametric Tests).
Sample Skewness and Kurtosis values can be obtained from SigmaXL’s descriptive statistics: SigmaXL > Statistical Tools > Descriptive Statistics.
A slight Skew is +/- 0.5, moderate Skew is +/- 1, severe Skew is +/- 2 and extreme Skew is +/- 5.The Skewness range used should be -5 to +5. Values beyond this range are extrapolated so may be inaccurate.
Kurtosis for a normal distribution is 0. Kurtosis must be greater than or equal to:
(Skew ^ 2 - 1.48).
Kurtosis “delta” is Kurt - Skew2 and is used in the regression equation. Kurtosis delta range should be -1.48 to +1.48. A kurtosis delta less than -1.48 denotes a bimodal distribution so this is a lower boundary. Values above +1.48 are extrapolated so may be inaccurate.
The calculator assumes that all samples have the same Skewness and Kurtosis.
The data for minimum sample size formulas are derived from extensive Monte Carlo simulations for n = 2 to 2000. Observed alpha values were determined empirically from the p-values of 100,000 replicate hypothesis tests for each n. Non-normal data with Skew = -5 to +5 and Kurt delta = -1.48 to +1.48 was generated using the Pearson Family function (see SigmaXL DiscoverSim Workbook: Appendix for details).
Minimum sample size for robustness occurs when the simulated observed alpha is within +/- 20% of the specified alpha (Bradley 1980 and Rhiel 1996).
A separate regression model was constructed for each hypothesis test, alternative hypothesis, and confidence level (total of 21 models), using coding as shown.

The model predictor terms are Skewness^2 and Kurtosis Delta. The response is n minimum. The term coefficient values are stored in the template as shown.
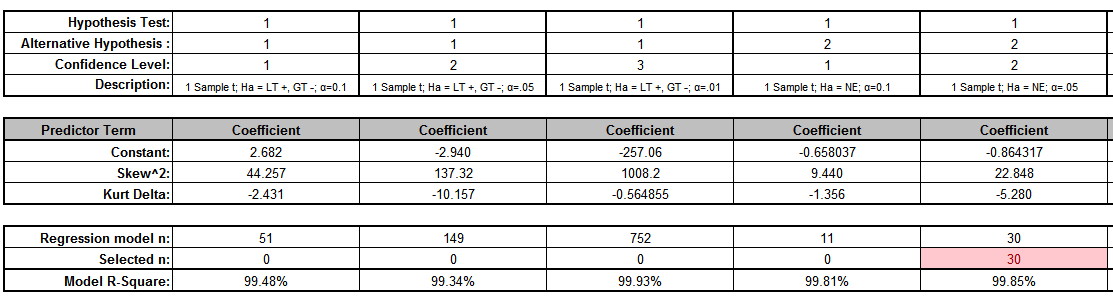
Model R-Square values are typically over 99%, with some exceptions (96%) due to small estimated sample sizes.
The model used is the one which matches the selected hypothesis test, alternative hypothesis, and confidence level. The selected n is highlighted in red and is also displayed in the template Results cell. If n > 2000, a text display “> 2000” is shown in the Results cell.
Boos, D.D. and Hughes-Oliver, J.M. (2000), “How Large Does n Have to be for Z and t Intervals?,” The American Statistician, 54(2), 121-128.
Bradley, J. V. (1980), “Nonrobustness in Z, t, and F Tests at Large Sample Sizes,” Bulletin of the Psychonomics Society, 16(5), 333-336.
Rhiel, G. S., and Chaffin, W. W. (1996), “An Investigation of the Large-Sample/Small-Sample Approach to the One-Sample Test for a Mean (Sigma Unknown),” Journal of Statistics Education, 4, No. 3 (www.amstat.org/publications/jse).
SigmaXL, Inc., DiscoverSim Version 1.1 Workbook.
Our CTO and Co-Founder, John Noguera, regularly hosts free Web Demos featuring SigmaXL and DiscoverSim
Click here to view some now!
Phone: 1.888.SigmaXL (744.6295)
Support: Support@SigmaXL.com
Sales: Sales@SigmaXL.com
Information: Information@SigmaXL.com